Topological Methods in Combinatorics and Extremal Set Theory

Zachary Munro

12:00, Friday, Oct. 11
BURN 1025



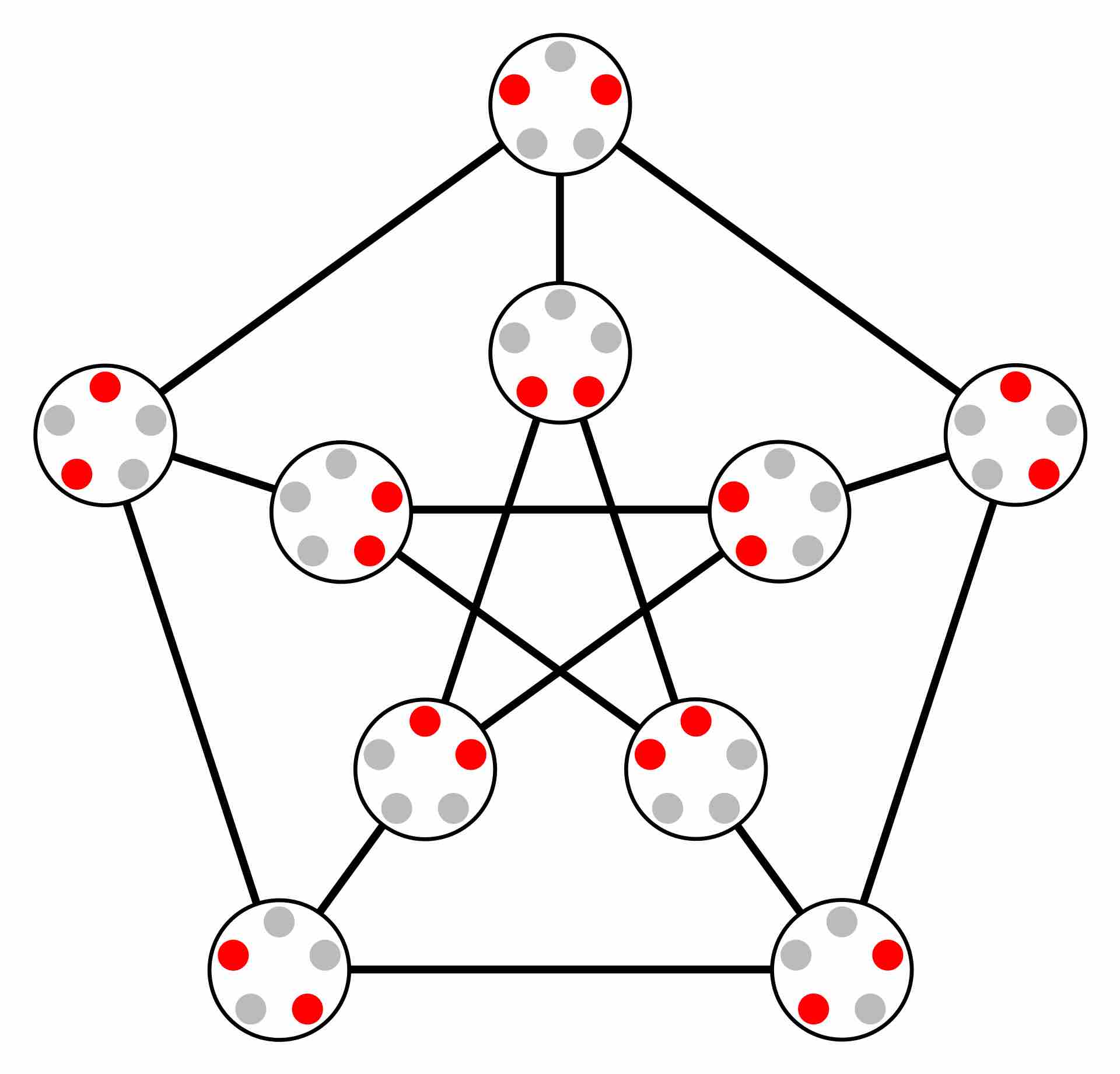
Extremal set theory is concerned with the behaviour of maximal collections of subsets which satisfy some intersection or containment condition. Simple motivating questions include: What is the largest number of $k$-element subsets of an $n$-element set which pairwise intersect? Or, what is the largest number of subsets of an $n$-element set in which no two subsets are comparable (by inclusion)?

We present a proof of the Erdos-Ko-Rado theorem, answering the first question. We then formulate the question which Kneser's (now proven) conjecture answers. After a slight detour to collect some topological tools, we give a proof of Kneser's conjecture by Joshua Greene.

All graduate students are invited. As with all talks in the graduate student seminar, this talk will be accessible to all graduate students in math and stats.

This seminar was made possible by funding from the McGill mathematics and statistics department and PGSS.

back