A priori bootstrap for computer-assisted proofs. We introduce in [13] a method based on piecewise polynomial interpolation to enclose rigorously solutions of nonlinear ODEs. Using a technique which we call a priori bootstrap, we transform the problem of solving the ODE into one of looking for a fixed point of a high order smoothing Picard-like operator. We then develop a rigorous computational method based on a Newton-Kantorovich type argument to prove existence of a fixed point of the Picard-like operator. Using this approach, we proved existence of several ballistic spiral orbits for ABC flows.

Stable and unstable manifolds of periodic orbits. In papers [2,3] we present a method for computing Fourier-Taylor expansions of un/stable manifolds attached to hyperbolic periodic orbits. From this method we obtain accurate representation of the invariant manifold as well as the dynamics on the manifold, it admits natural a-posteriori error analysis, and it does not require numerical integration of the vector field. Our approach is based on the Parameterization Method for invariant manifolds, and studies a certain PDE which characterizes a chart map of the manifold. The method requires only that some mild non-resonance conditions hold. In paper [2] we exploit the Floquet normal form in order to efficiently compute the Fourier-Taylor expansion. Computations of cycle-to-cycle connecting orbits which exploit these manifolds are also discussed. In paper [3], we present an a-posteriori Theorem which provides mathematically rigorous error bounds for the high order Fourier-Taylor parameterizations of the manifolds. We validate computations of some 2D manifolds in R^3 and a 3D manifold in R^4.

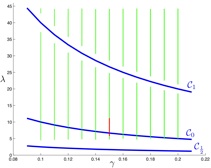
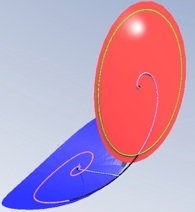
[1] R. Castelli and J.-P. Lessard. Rigorous numerics in Floquet theory: computing stable and unstable bundles of periodic orbits. SIAM Journal on Applied Dynamical Systems, 12(1): 204–245, 2013. (pdf)

[2] R. Castelli, J.-P. Lessard and J.D. Mireles James. Parameterization of invariant manifolds for periodic orbits (I): efficient numerics via the Floquet normal form, SIAM Journal on Applied Dynamical Systems, 14(1): 132-167, 2015. (pdf)

[3] R. Castelli, J.-P. Lessard and J.D. Mireles James. Parameterization of invariant manifolds for periodic orbits (II): a-posteriori analysis and computer assisted error bounds, Journal of Dynamics and Differential Equations, 2017. (pdf)

[4] M. Breden, J.-P. Lessard and J.D. Mireles James. Computation of maximal local (un)stable manifold patches by the parameterization method. Indagationes Mathematicae, 27(1): 340-367, 2016. (pdf)

[5] J.-P. Lessard, J.D. Mireles James and C. Reinhardt. Computer assisted proof of transverse saddle-to-saddle connecting orbits for first order vector fields. Journal of Dynamics and Differential Equations, 26(2): 267-313, 2014. (pdf)

[6] J.-P. Lessard and C. Reinhardt. Rigorous numerics for nonlinear differential equations using Chebyshev series. SIAM Journal on Numerical Analysis, 52(1): 1-22, 2014. (pdf)

[7] A. Correc and J.-P. Lessard. Coexistence of nontrivial solutions of the one-dimensional Ginzburg-Landau equation: a computer-assisted proof, European Journal of Applied Mathematics, 26(1): 33-60, 2015. (pdf)

[8] A. Hungria, J.-P. Lessard and J.D. Mireles James. Rigorous numerics for analytic solutions of differential equations: the radii polynomial approach, Mathematics of Computation, 85 (299): 1427–1459, 2016. (pdf)

[9] L. d’Ambrosio, J.-P. Lessard and A. Pugliese. Blow-up profile for solutions of a fourth order nonlinear equation, Nonlinear Analysis: Theory, Methods and Applications, 121: 280-335, 2015. (pdf)

[10] J.-P. Lessard, J.D. Mireles James and J. Ransford. Automatic differentiation for Fourier series and the radii polynomial approach, Physica D, 334: 174-186, 2016. (pdf)

[11] M. Breden, L. Desvillettes and J.-P. Lessard. Rigorous numerics for nonlinear operators with tridiagonal dominant linear parts, Discrete and Continuous Dynamical Systems: Series A, 35(10): 4765-4789, 2015. (pdf)

[12] M. Gameiro, J.-P. Lessard and Y. Ricaud. Rigorous numerics for piecewise-smooth systems: a functional analytic approach based on Chebyshev series. Journal of Computational and Applied Mathematics, 292: 654-673, 2016. (pdf)

[13] M. Breden and J.-P. Lessard. Polynomial interpolation and a priori bootstrap for computer-assisted proofs in nonlinear ODEs, To appear in Discrete and Continuous Dynamical Systems - Series B. (pdf)

[14] J.-P. Lessard. Rigorous verification of saddle-node bifurcations in ODEs. Indagationes Mathematicae, 27(4): 1013-1026, 2016. (pdf)

Transverse intersections of stable and unstable manifolds. A method for proving existence of saddle-to-saddle connections between equilibria of ODEs is introduced in [5]. The first step consists of rigorously computing high order parametrizations of the local un/stable manifolds. If the manifolds intersect, the Newton-Kantorovich theorem is used to validate the existence of a short connecting orbit. If the manifolds do not intersect, a BVP with boundary values in the local manifolds is rigorously solved by a contraction mapping argument on a ball centered at the numerical solution, yielding the existence of a long connecting orbit. In both cases our argument yields transversality of the corresponding intersection of the manifolds. The method is applied to the Lorenz equations, where a study of a pitchfork bifurcation with saddle-to-saddle stability is done and where several proofs of existence of short and long connections are obtained.

Tridiagonal dominant operators. We propose in [11] a method to compute solutions of infinite dimensional nonlinear operators f(a)=0 with tridiagonal dominant linear parts. We recast the operator equation into an equivalent Newton-like equation T(a)=a-Af(a), where A is an approximate inverse of the derivative operator Df(ā) at an approximate solution ā. We develop rigorous computer-assisted bounds to show that T is a contraction near ā, which yields existence of a solution. Since Df(ā) does not have an asymptotically diagonal dominant structure, the computation of A is not straightforward. This work provides a method to obtain A and proposes a new rigorous computational method to prove existence of solutions of equations with tridiagonal dominant linear derivatives.

Automatic differentiation and Fourier series. In [10] we implement a computer-assisted technique for proving existence of periodic solutions of nonlinear differential equations with non-polynomial nonlinearities. We exploit ideas from the theory of automatic differentiation in order to formulate an augmented nonlinear system which has only polynomial nonlinearities. We validate the computation of periodic orbits for the augmented system using a combination of Fourier series analysis and the radii polynomial approach. As applications we present the details and a number of computer-assisted results for the classical Lyapunov family of orbits in the Planar Circular Restricted Three-Body Problem (PCRTBP).

Analytic solutions of ODEs. In [8] we adapt the method of radii polynomials to the analytic category, which had been previously only developed in the C^k category. For ease of exposition we focus on studying periodic solutions in Cartesian products of infinite sequence spaces. We derive the radii polynomials for some specific application problems (equilibrium solutions in the Swift-Hohenberg equation and periodic orbits in the Lorenz equations), and give a number of computer assisted proofs in the analytic framework.

Piecewise-smooth dynamical systems. A rigorous computational method to compute solutions of piecewise-smooth systems using a functional analytic approach based on Chebyshev series is introduced in [12]. A general theory, based on the radii polynomial approach, is proposed to compute crossing periodic orbits for continuous and discontinuous (Filippov) piecewise-smooth systems. Explicit analytic estimates to carry the computer-assisted proofs are presented. The method is applied to prove existence of crossing periodic orbits in a model nonlinear Filippov system and in the Chua’s circuit system. A general formulation to compute rigorously crossing connecting orbits for piecewise-smooth systems is also introduced.

Rigorous numerics via Chebyshev series. A method based on Chebyshev series is proposed in [6] to rigorously compute solutions of IVP and BVP of nonlinear vector fields. The idea is to recast solutions as fixed points of an operator defined on a Banach space of fast decaying Chebyshev coefficients and to use the radii polynomials to show the existence of a unique fixed point nearby an approximate solution. As applications, solutions of initial value problems in the Lorenz equations and symmetric connecting orbits in the Gray-Scott equation are rigorously computed. The symmetric connecting orbits are obtained by solving a boundary value problem with one of the boundary values in the stable manifold.

Blow-up profile of solutions in a fourth order nonlinear equation. It is well known that the nontrivial solutions of the equation u′′′′+κu′′+f(u)=0 blow up in finite time under suitable hypotheses on the initial data, κ and f (the equation is commonly referred to as extended Fisher-Kolmogorov or Swift-Hohenberg). These solutions blow up with large oscillations. Knowledge of the blow-up profile of these solutions is important in studying the dynamics of suspension bridges. In paper [9] we provide details of the blow-up profile. The key idea is to relate this blow-up profile to the existence of periodic solutions for an auxiliary equation.

Coexistence of solutions in the Ginzburg-Landau model. In paper [7], we settle a 30 years old conjecture raised by Seydel in [Numer. Math., 41(1):93-116, 1983] about coexistence of as many as seven solutions of the Euler-Lagrange equations for the one-dimensional Ginzburg-Landau model of superconductivity. The idea is to recast solutions as fixed points of a Newton-like operator defined on a Banach space of rapidly decaying Chebyshev coefficients. Analytic estimates, the radii polynomials and the contraction mapping theorem are combined to show existence of solutions nearby numerical approximations.

Stable and unstable linear bundles of periodic orbits. In [1], a method to compute Floquet normal forms of fundamental matrix solutions of non-autonomous linear differential equations with periodic coefficients is introduced.  The Floquet normal form of a fundamental matrix solution Φ(t) is a canonical decomposition Φ(t)=Q(t)e^(Rt), with Q(t) a real periodic matrix and R a constant matrix. To compute the Floquet normal form, we use the regularity of Q(t) and solve simultaneously for R and Q(t) with the contraction mapping theorem in a Banach space of rapidly decaying Fourier coefficients. The explicit knowledge of R and Q(t) can then be used to construct, in a rigorous computer-assisted way, stable and unstable bundles of periodic orbits of vector fields.

Maximizing the image of the manifolds. In [4], we develop some automatic procedures for computing high order polynomial expansions of local (un)stable manifolds for equilibria of differential equations. Our method incorporates validated truncation error bounds, and maximizes the size of the image of the polynomial approximation relative to some specified constraints. More precisely we use that the manifold computations depend heavily on the scalings of the eigenvectors: indeed we study the precise effects of these scalings on the estimates which determine the validated error bounds.  This relationship between the eigenvector scalings and the error estimates plays a central role in our automatic procedures. In order to illustrate the utility of these methods we present several applications, including visualization of invariant manifolds in the Lorenz and FitzHugh-Nagumo systems and an automatic continuation scheme for (un)stable manifolds in a suspension bridge problem.

Rigorous verification of saddle-node bifurcations in ODEs. We introduce in [14] a general method for the rigorous verification of saddle-node bifurcations in ordinary differential equations. The approach is constructive in the sense that we obtain precise and explicit bounds within which the saddle-node bifurcation occurs. After introducing a set of sufficient generic conditions, an algorithm to verify rigorously the conditions is introduced. The approach is applied to prove existence of some saddle-node bifurcations in the Hodgkin-Huxley model.

Contact

Department of Math. and Stat.

McGill University

Burnside Hall, Room 1119

805 Sherbrooke West

Montreal, QC, H3A 0B9, CANADA

jp.lessard@mcgill.ca

Phone: (514) 398-3804

Positions Available

@ Ph.D. level:

1. • I recommend that you read some of my papers before contacting me.
   

2. • I will not reply to generic emails.
   

@ Postdoc level:

1. • Openings are available through the
   CRM-ISM Postdoctoral program.

Jean-Philippe Lessard

Associate Professor

McGill University

Department of Mathematics and Statistics

Research Projects